カテゴリカルデータ解析

エグザメトリカのカテゴリカルデータ解析では，以下の統計指標を出力します．

l 閾値

l 平均情報量（エントロピー）

l 項目得点双列相関（バイシリアル相関）・項目得点多列相関（ポリシリアル相関）

l 項目間四分相関（テトラコリック相関）・項目間多分相関（ポリコリック相関）

閾値

l ２値データ

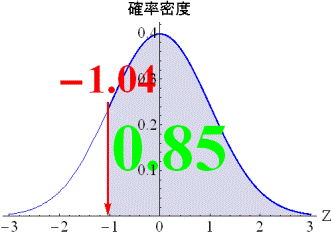
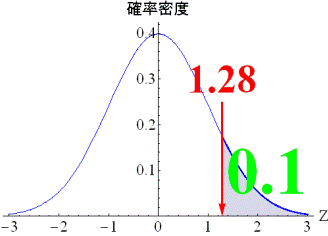
まず，データの背後に標準正規分布を仮定します．そのうえで，たとえば，左の図のように，正答率が0.85であるような項目の閾値は-1.04となります．閾値は，閾値以上の面積が正答率と等しくなるように求まります．左の項目は，標準正規分布のもとで能力が-1.04以上の受検者が正答できるような易しい項目であると解釈できます．一方，右の図は，正答率が10%の項目について表しています．このとき閾値は1.28となり，標準正規分布のもとで1.28以上の高い能力でないとその項目に正答できないと解釈します．

l 多値データ

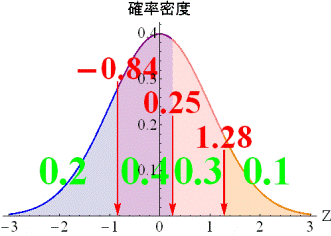
多値の場合の閾値は，2値のときの単純な拡張です．カテゴリ数がK個のとき，閾値はK-1個あります．いま，順序カテゴリ数が4つある項目があり，選択率がそれぞれ(0.2 0.4 0.3 0.1)だったとします．そのとき，3つの閾値は，標準正規分布の面積を分割して上述の選択率となるように閾値が決まります．

平均情報量（エントロピー）

平均情報量は，カテゴリデータ（質的データ）の分散のような指標です．受検者の選択が，あるカテゴリに集中すると，平均情報量は0に近づきます．一方で，被験者のカテゴリ選択が散らばる（集中しない）ほど，平均情報量の値は大きくなります．データの散らばりの指標は，連続データの散らばりの大きさには，標準偏差や分散を使えばよいですが，質的データには，平均情報量を用いてデータの散らばりの大きさを確認します．一般に，カテゴリ選択が集中するような項目は，質問してもしなくても同じことですので無情報です．平均情報量のとても小さい項目は，項目として適切でないことが多いです．

双列相関（バイシリアル相関）・多列相関（ポリシリアル相関）

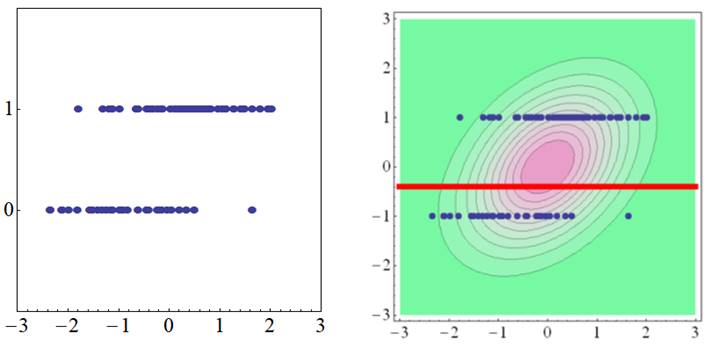
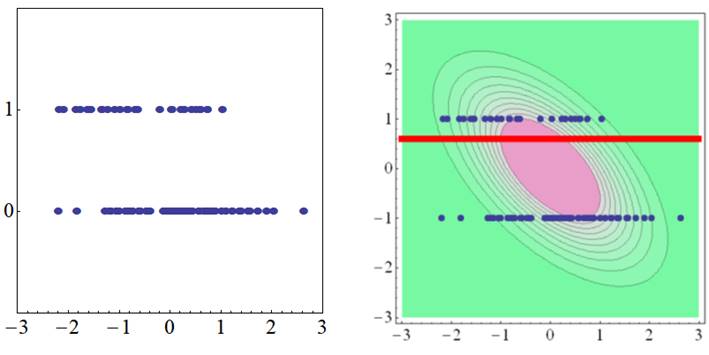
l 双列相関（2値変数×連続変数）

2値の順序カテゴリカルデータと連続データの背後に，2変量標準正規分布を仮定し，もっともデータの生起確率が高まるように2変量正規分布の相関係数を求めます．そのようにして求められた相関係数を双列相関係数と呼びます．

上の図では，Y軸の2値データが1のときのほうが，X軸変数が高くなる弱い傾向があります．そのようなとき，2変数のデータの背後に，中程度の相関をもつ2変量標準正規分布が当てはまります．また，若干，Y軸の2値変数が1となるほうが，データの観測数が多いので，閾値（赤線）が2変量正規分布のピークの少し下に来ています．

上の図では，Y軸変数が0であるときのほうが，X軸の連続変数が大きくなる傾向があるので，2変数の背後には，負の相関をもつ2変量正規分布が当てはまります．このように，どのような相関係数をもつ2変量正規分布が最もデータに当てはまるか，という観点から求められた相関係数が双列相関係数です．2値データを連続データと見なしてピアソン相関を算出するよりも妥当な相関係数が求まります．

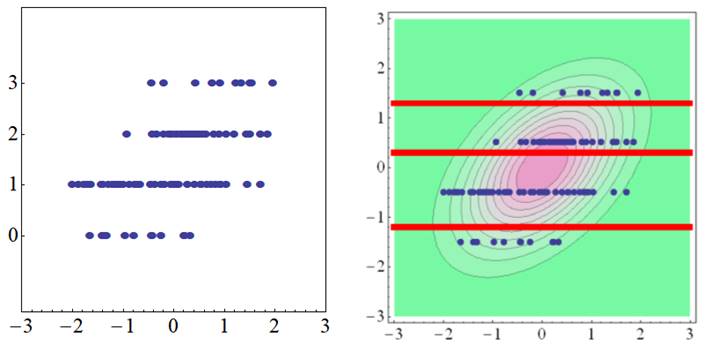
l 多列相関（多値変数×連続変数）

双列相関係数を多値の場合に拡張したものを多列相関です．重列相関と呼ぶ場合もあります．心理質問紙で多く使われているリッカート尺度データは，厳密に言えば間隔が一定でない順序カテゴリカルデータです．したがって，3件法や4件法など件数が少ないリッカートデータは，連続データと見なさずに順序カテゴリカルデータとして扱った方がよいでしょう．

四分相関（テトラコリック相関）・多分相関（ポリコリック相関）

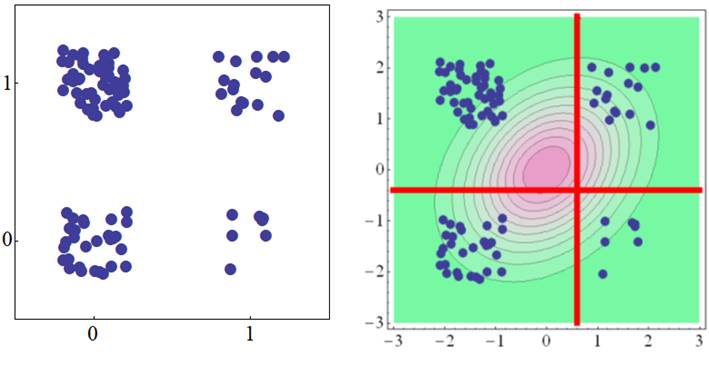
l 四分相関（2値変数×2値変数）

左上と左下の散布図は，2つの2値変数の散布図です．データの数が分かるように，わざとデータを散らしています．この2つの変数の背後に，2変量標準正規分布を仮定して，データの生起確率が最も高くなるように求めた相関係数を四分相関と言います．

上の図では， X軸の2値変数が0のときのほうがデータ数が大きいので，まずX軸の閾値（縦の赤線）が2変量正規分布のピークよりも正の方向に位置します．また，Y軸の2値変数が1のときのほうがデータ数が大きいのでY軸の閾値（横の赤線）がピークよりも負に下がります．そのうえで，4分割されたデータのうち，(1,1)と(0,0)のデータ数の方が，(0,1)と(1,0)のデータよりも少し多いので，四分相関が正となって求まります．

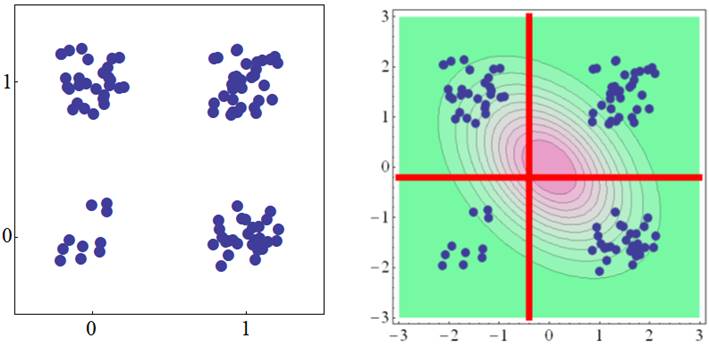
逆に，上の図では(1, 0)と(0, 1)のデータ数の方が，(1, 1)と(0, 0)のデータ数よりも多いので，このデータの背後にある2変量正規分布は負の相関をもつほうが，このデータが発生しやすくなります．したがって，このような状況では，四分相関が負となって求まります．

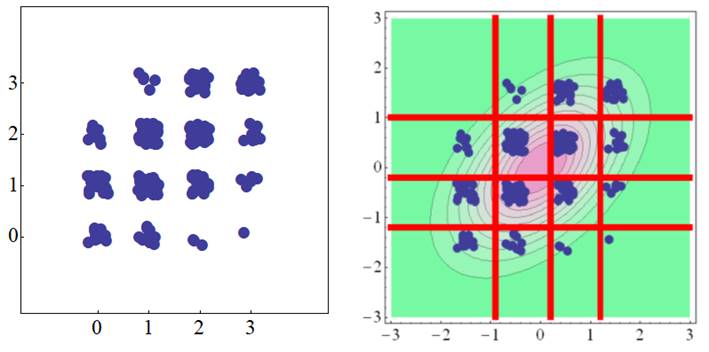
l 多分相関（多値変数×多値変数）

四分相関を多値のカテゴリカル変数同士の相関に拡張したものが多分相関です．心理質問紙などでよくみられるリッカート尺度データは，厳密に言えば，間隔が等間隔ではないので，3件法や4件法など件数が小さいときは，連続データと見なして相関係数を求めるよりも，順序カテゴリカルデータと見なしたほうが妥当な相関係数が求まります．